Comme tant d’autres peuples traditionnels, les Celtes ont eu un souci presque obsessionnel de la structuration de l’espace. La préoccupation du repérage par rapport à l’horizon, par rapport aux directions solsticiales et équinoxiales, la quadripartition liée aux points cardinaux, la sacralisation du centre sont des faits bien connus. La pierre de Kermaria, dont tous les motifs sont quaternaires, peut ici servir d’emblème.

Mais les Celtes, et plus particulièrement peut‑être les Gaulois de Gaule cisalpine et transalpine, sont allés bien au‑delà de ces repérages simples. À l’échelle locale, les recherches menées sur les troménies bretonnes par Donatien Laurent ou Joël Hascouët (1995 et 2002), sur la région de Larchant par Claude Maumené (2009), ou sur la région de Rennes par le regretté Marc Déceneux (2010), montrent la précision et la subtilité d’organisations topographiques que la persistance de certaines traditions permet encore de décrypter. Il y a là un vaste champ de recherches largement ouvert. Cependant, les Gaulois ne se contentaient pas de structurer leur petit espace local. César nous dit qu’entre autres domaines de préoccupations, les druides discutaient beaucoup de la dimension du monde et des territoires1. Si l’on ne se contente pas de traduire classiquement terrarum par « la Terre », induisant de vagues spéculations mythiques, et si l’on redonne au pluriel sa pleine valeur de « territoires », on est conduit à supposer des préoccupations quantitatives de mesure du paysage, autrement dit de géodésie.

Ils ne partaient pas de rien. On songe à une influence possible de la Grèce, où la géographie s’est développée assez rapidement à partir du v^e siècle, — à l’héritage de Pythéas, capable au iv^e siècle avant notre ère de calculer la latitude de Marseille à un dixième de degré près, aux exploits d’Ératosthène —, sans parler de ce qu’ils ont pu apprendre au contact des Étrusques, grands maîtres de l’orientation des cités.

On sait comment procède la géodésie moderne : par triangulation et calcul trigonométrique. Les Anciens s’efforçaient en première approximation de ramener les grands ensembles géographiques à des figures géométriques simples2 : carrés, rectangles et surtout triangles. La construction de triangles aux propriétés connues pouvait leur permettre, la longueur d’un côté ayant été mesurée, de connaître la longueur des deux autres. Il en allait ainsi du triangle équilatéral, du triangle dit « platonicien » (moitié d’un équilatéral, où la longueur du petit côté de l’angle droit vaut donc la moitié de l’hypoténuse) et de triangles rectangles depuis longtemps repérés : triangle dit de Pythagore (surtout utilisé pour la construction d’angles droits), triangle rectangle isocèle, triangle 1 x 2 où le petit côté de l’angle droit vaut la moitié du grand, triangle 3/8… Une mention spéciale doit être faite du triangle rectangle dit « égyptien » ou « pyramide », dont le rapport du grand au petit côté de l’angle droit est de 10/9 et le rapport de l’hypoténuse au grand côté de 14/11, soit dans les deux cas 1,272…3. Nous retrouverons plus loin ces différents triangles.

Sur le terrain, les Anciens, et particulièrement les Gaulois, semblent avoir construit ce type de figures en déterminant des directions à partir de sites géographiques remarquables. Des visées peuvent atteindre des centaines de kilomètres par repérage à vue, avec l’aide de feux allumés sur les sommets (moyen qui servait aussi à transmettre les nouvelles, comme on le voit au début de l’Agamemnon d’Eschyle). Des observations astronomiques pouvaient également entrer en jeu : levers ou couchers du Soleil et de la Lune à certaines dates, lever héliaque de certaines étoiles… Ces visées diversement orientées étaient, au sens propre, recroisées par les directions cardinales, axes N‑S et axes des équinoxes.

Au cours de recherches déjà fort longues, et dont j’ai déjà eu l’occasion de parler devant les Amis des Études celtiques il y a cinq ans, j’ai formulé l’hypothèse que le toponyme Mediolanum (que Joseph Loth avait rapproché dès 1915 de la notion d’omphalos, et que Xavier Delamarre propose de traduire par « plein milieu ») pouvait désigner des points de repère dans une vaste entreprise de géodésie sacrée — qui pour être sacrée n’en était pas moins précise. Les toponymes français issus de Mediolanum (Molain, Maulain, Meilhan, etc.) ont été depuis longtemps plus ou moins complètement répertoriés (Longnon, 1887 ; Holder, 1896‑1913 ; Berthoud, 1924 ; Vincent, 1937 ; Guyonvarc’h, 1961 ; Vadé, 1974 et 2000 ; Lacroix, 2007). On peut y adjoindre d’assez nombreux micro-toponymes marquant le milieu, tels que Milan, Moyen, Montmoyen, Molien, etc., de même que les Méjean et Méjane du pays d’oc. La présence de ces micro-toponymes ne suffit pas à faire preuve, mais vaut d’être notée lorsque ces hameaux ou ces lieux-dits se situent sur une des lignes des Mediolanum principaux qu’ils semblent baliser.

Mais les Mediolanum ne sont peut‑être pas les véritables points de départ de l’entreprise. Ils m’apparaissent de plus en plus clairement comme des points de convergence de visées dont les points de départ sont assez naturellement des lieux hauts (et des hauts lieux). Trois de ces observatoires naturels sont à situer d’emblée : la Montagne de Dun dans le Brionnais, le Puy-de-Dôme et le Mont Dardon au sud de Bibracte.

Plaçons au départ, presque à titre de mythe d’origine, la ligne reliant le pays des Bituriges, celui des Éduens et la ville de Mediolan(i)um devenue Milano, chez les Insubres d’Italie. On connaît le récit historico-mythique de Tite-Live (V, 33‑35), qui donne l’initiative du transfert de peuples au roi des Bituriges, mais qui attribue finalement aux Éduens le choix de l’emplacement de la nouvelle ville : « Apprenant que le pays où ils s’étaient installés s’appelait Insubrium, du même nom que le canton des Insubres chez les Éduens, ils obéirent au présage tiré de la localité et fondèrent une ville qu’ils appelèrent Mediolanum. » C’est donc principalement une affaire entre Éduens, Insubres et Bituriges, qui en tant que « Rois du monde » se jugeaient sans doute qualifiés pour se situer au centre.

En territoire biturige, autrement dit en Berry, on connaît deux localités dont le toponyme dérive d’un ancien Mediolanum : Châteaumeillant près de Saint-Amand-Montrond, et Meillant, l’une et l’autre dans le département du Cher. Je placerai au début de mon exposé Châteaumeillant et je l’achèverai par Meillant. D’une certaine manière, tout mon discours consistera à passer de l’un à l’autre.

Châteaumeillant bénéficie à peu près sûrement d’une antériorité chronologique. C’est un des rares Mediolanum qui puisse être daté, grâce aux fouilles effectuées à partir de 1956 et poursuivies actuellement par Sophie Krausz. La mise en place d’un habitat gaulois est datée par S. Krausz d’environ 200 ans avant notre ère. Le croisement de plusieurs routes et le nombre incroyable d’amphores vinaires (datant du dernier tiers du ii^e siècle) qu’on y a retrouvées donne une idée de son importance commerciale.

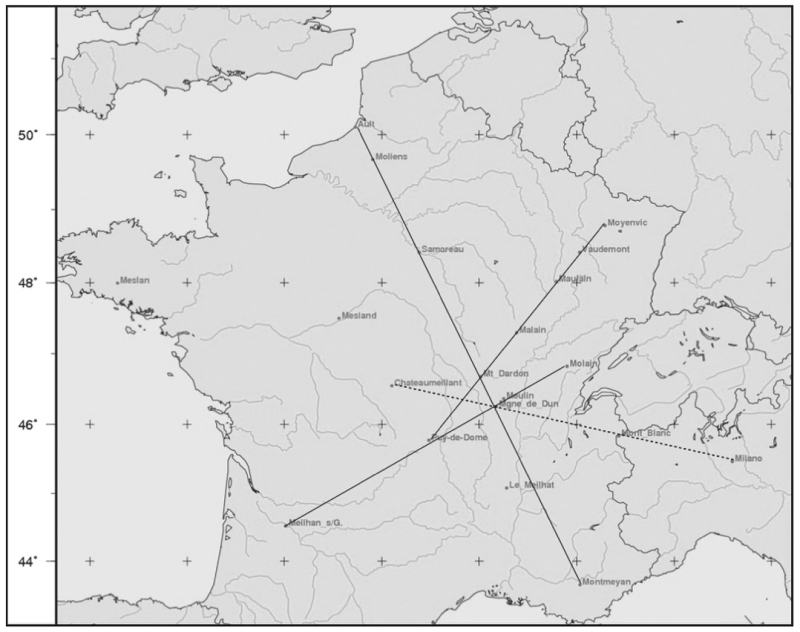
Traçons donc une ligne de Châteaumeillant à Milano (carte ci‑contre). Ce sera notre ligne de base (portée en tiretés sur la carte ci‑jointe en projection de Mercator4). Partant de Milano, on constate que cette ligne traverse le Tessin aux alentours de Turbigo, passe par le Mont Blanc (fameux point de repère !), puis au sud de Nantua et de Bourg-en-Bresse chez les Ambarres, clients des Éduens à l’époque de César, pour arriver à la Montagne de Dun dans le Brionnais, à la frontière du territoire éduen et de leurs clients, les Ségusiaves.

Le double sommet de la Montagne de Dun est visible depuis le Puy-de-Dôme : on peut en lire le nom sur la table d’orientation au sommet du Puy. Et depuis la Montagne de Dun, le Mont Blanc est visible par temps favorable. C’est un site qui a été puissamment fortifié au Moyen Âge et qui jouit encore de nos jours d’un prestige particulier dans le pays. Mais il y a des raisons bien précises, que l’on va voir dans un instant, qui conduisent à considérer Dun (utilisons cette abréviation) comme une sorte d’observatoire gaulois — en tout cas éduen — de première importance.

Chez les Arvernes, le Puy-de-Dôme offre à l’évidence un autre point de repère et d’orientation privilégié. Il n’est pas nécessaire de rappeler son caractère sacré à l’époque gauloise et gallo-romaine — caractère dont témoignent encore les ruines de l’immense temple édifié en l’honneur de Mercure Dumias.

Carte de localisation.

Le Mont Dardon, à 26 km au sud exact du Mont Beuvray, semble également avoir joué un rôle important dans cette entreprise de géodésie. On verra tout à l’heure pourquoi. C’est lui aussi un site d’observation privilégié. Le Pr Carole Crumley, qui a effectué pendant plusieurs années des fouilles au Mont Dardon (occupé depuis l’époque du Bronze), parle de « la vue spectaculaire qu’il permet vers le nord sur le Morvan, au sud sur la vallée de la Loire et le Massif central et, par temps clair, à l’est jusqu’au Mont Blanc » (Crumley, 1993).

Ces trois sites dessinent un triangle dont chaque côté peut être considéré comme le germe, le segment de départ de lignes beaucoup plus étendues. Je les indique par anticipation sur la carte ci‑jointe. Certes, à une échelle plus précise, on constate que ces alignements connaissent parfois des inflexions : il en va ainsi de vieilles poutres, qui sans avoir la rectitude de poutrelles d’acier ou de droites tracées par ordinateur, n’en permettent pas moins de lire parfaitement le dessin général d’une charpente.

• Le côté Puy-de-Dôme : Dun se prolonge (moyennant une légère distorsion) en direction du sud-ouest jusqu’à la Garonne qu’il rejoint à Meilhan-sur-Garonne, en direction du nord-est jusqu’à Molain dans le Jura, en bordure de la forêt des Moisdons.

• Le côté Dun : Dardon est le point de départ d’une immense diagonale qu’on nommera la « grande Diagonale ». Vers le nord, la ligne passe par le site de Montmélian, dominant la Seine à Samoreau (nous le désignerons par le simple toponyme de « Samoreau »), puis par Moliens dans l’Oise, avant de rejoindre la côte à Ault (étymologiquement : « la hauteur ») — site géographiquement remarquable qui marque la frontière entre la côte normande bordée de falaises et la baie de Somme.

Vers le sud, la ligne peut être prolongée jusqu’au village perché de Montmeyan dans le Var.

• Indiquons tout de suite que le Mont Dardon se situe à mi‑distance de Moliens (372 km) et de Montmeyan (374 km).

• Enfin le côté Puy-de-Dôme : Dardon rejoint au nord-est les anciens Mediolanum de Mâlain (Côte‑d’Or), de Maulain (Haute-Marne), pour arriver au village de Moyenvic (« le village du milieu », près de Château-Salins dans la Moselle).

Depuis la Montagne de Dun

Ces grandes lignes étant indiquées, revenons à Dun et aux points les plus importants de ce dispositif, qui en comporte bien d’autres dont le détail entraînerait des développements ici hors de proportion.

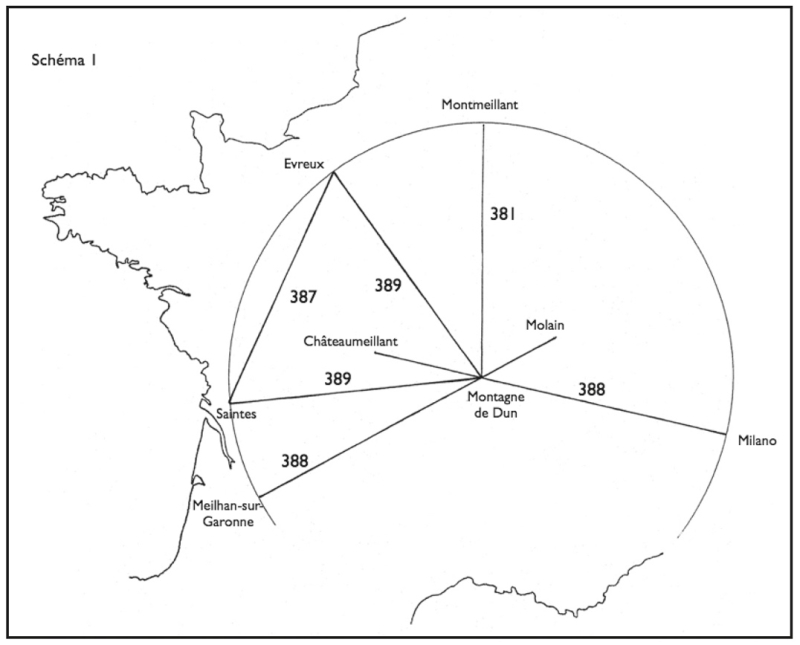
À partir de la Montagne de Dun apparaît un jeu d’équidistances stupéfiant, dont l’évidence s’impose (fig. 1) :

• Milano – Dun = 388 km ;

• Dun – Saintes (Mediolanum Santonum) = 389 km ;

• Dun – Évreux (Mediolanum Aulercorum) = 389 km ;

• de plus Saintes – Évreux = 387 km, d’où un immense triangle équilatéral Dun – Saintes – Évreux ;

• enfin Dun – Meilhan-sur-Garonne = 388 km5.

Figure 1.

Une telle précision, à la fois dans les distances et dans les orientations, ne peut être purement aléatoire. Cette gerbe d’équidistances justifierait à elle seule une recherche portant sur l’existence d’un système de repérage à grande échelle et, ultérieurement, sur les moyens mis en œuvre pour y parvenir.

Meilhan-sur-Garonne

Il faudrait avoir le temps de s’attarder sur les caractéristiques géographiques et historiques de Meilhan-sur-Garonne, magnifique site d’éperon barré, devenu au Moyen Âge une importante cité fortifiée, mais je passe rapidement.

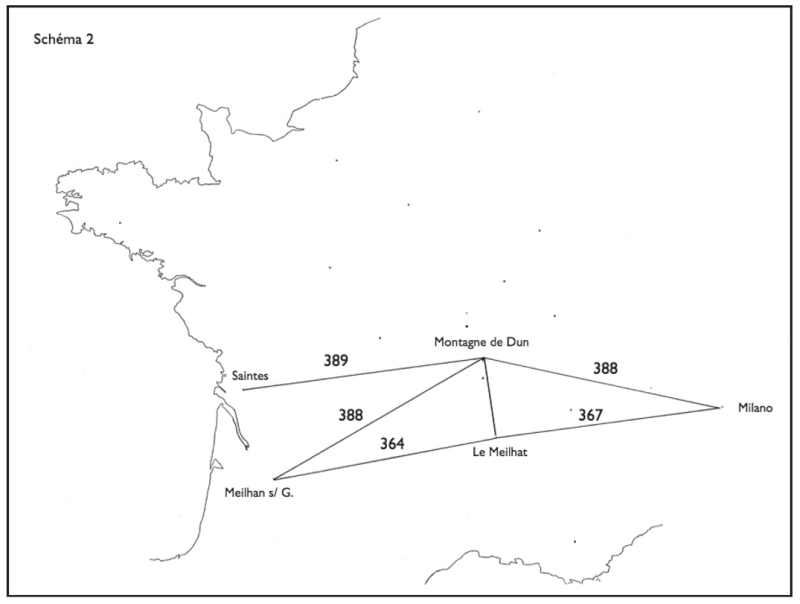
Du point de vue géométrique, la construction de Meilhan-sur-Garonne correspond à celle d’un triangle rectangle très allongé, symétrique du triangle formé par Milano, Dun et un point qui se situerait au milieu de l’immense ligne reliant Milano à Meilhan-sur-Garonne (fig. 2).

Figure 2.

J’ai été curieux de voir si ce milieu était marqué par un toponyme significatif. D’après la carte, le point correspondrait à un village de l’Ardèche nommé Pailharès (village ancien, probablement fortifié dès l’époque romaine). Or à Pailharès, j’ai eu la surprise de découvrir, sur la carte IGN au 1/20 000, un lieu-dit Le Meilhat : seul toponyme de type medio- à une centaine de kilomètres à la ronde, sauf une Roche du Milieu à Saint-Pierre-sur-Doux, à 9 km au nord-ouest du Meilhat, dans la direction du Puy-de-Dôme. (Sur place, Le Meilhat est le nom d’une maison à l’écart du village, adossée à des hauteurs où se trouvait peut‑être le véritable point d’observation.)

L’équidistance est exacte à quelques kilomètres près : 730 / 2 = 365 ; Milano – Le Meilhat = 366,7 km ; Le Meilhat – Meilhan-sur-Garonne = 363,6 km.

Une vérification précise montre que pour se situer exactement sur la ligne Milano – Meilhan-sur-Garonne, Le Meilhat devrait se trouver quelques kilomètres plus au sud. L’approximation n’en reste pas moins remarquable. J’ajoute qu’une fois les Alpes franchies (au sud du Gran Paradiso), plusieurs toponymes pourraient marquer les étapes d’un repérage entre Milano et Le Meilhat : un Montmélian à Bessans (Savoie) au bord de la rivière de l’Arc, un ruisseau de Miolan à Montricher-Albanne et, quelques kilomètres plus loin, un Plan Meillant à Fontcouverte-la-Toussuire. Le Rhône est atteint à Larnage, où Holder signale un ruisseau Milan (introuvable sur place).

Meilhan-sur-Garonne se trouve à la frontière des Bituriges Vivisques, des Vasates de la région de Bazas et des Nitiobroges, gens d’Agen. Historiquement, la détermination de Meilhan pourrait être en rapport avec l’installation des Bituriges Vivisques dans la région de Bordeaux : il faudrait être sûr de la date de cette installation. Meilhan-sur-Garonne semble obéir en tout cas à une sorte de principe de symétrie, dont on va voir d’autres témoignages. Géométriquement, et donc symboliquement dans ce type de pensée, c’est un autre Milano, par rapport à l’axe de symétrie que forme la ligne Dun – Le Meilhat.

Bissectrice

Revenons à Châteaumeillant, dans le prolongement de Milano – Dun. La presque équidistance Dun – Évreux = Dun – Meilhan-sur-Garonne entraîne celle de Châteaumeillant – Évreux = Châteaumeillant – Meilhan-sur-Garonne. En d’autres termes, la ligne Milano – Dun – Châteaumeillant est presque bissectrice de l’angle Évreux – Milano – Meilhan-sur-Garonne (l’angle vers Évreux étant légèrement plus ouvert que l’angle vers Meilhan). Tous les points de cette ligne sont donc quasi équidistants d’Évreux et de Meilhan-sur-Garonne (fig. 3).

Figure 3.

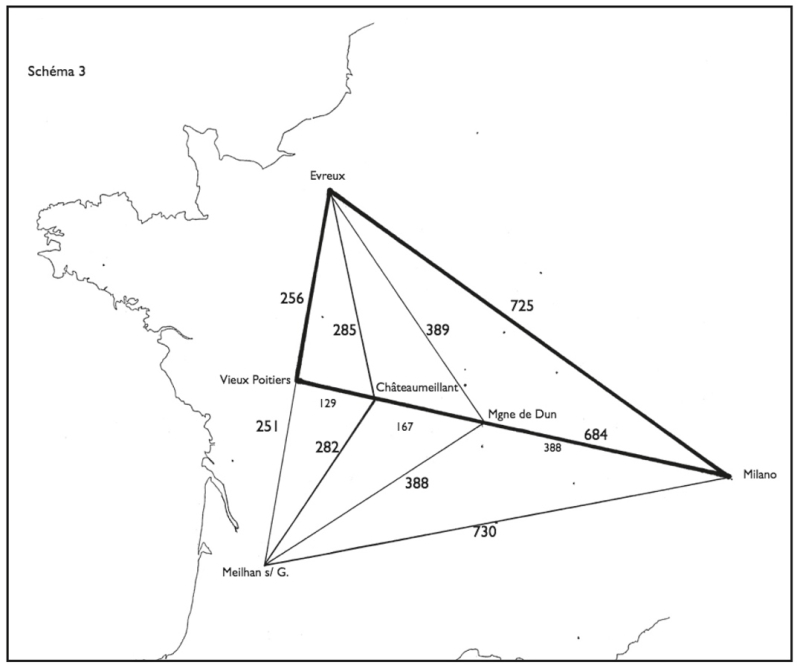
Si l’on relie Meilhan-sur-Garonne à Évreux (par une ligne dont l’importance va se confirmer de mieux en mieux) et si l’on prolonge la ligne de base au‑delà de Châteaumeillant jusqu’à sa rencontre avec cette ligne Évreux – Meilhan, on arrive à la Vienne, à 2,8 km de l’important site archéologique du Vieux-Poitiers.

Géométriquement, l’immense triangle Milano – Évreux – Vieux-Poitiers, ou plus exactement Vienne, est un exemple de ce que j’ai appelé un triangle rectangle 3/8, autrement dit dont les côtés de l’angle droit sont dans un rapport de 3 à 8 :

• • Vienne – Évreux = 256,5 km ; (256,5 / 3 = 85,5) ;

  • Milano – Vienne = 684 km ; (684 / 8 = 85,5).

La connaissance de la distance d’Évreux à la Vienne près de son confluent avec la Claise (distance importante mais qu’il n’est pas impensable de mesurer) permettrait donc de connaître la distance de la Vienne à Milano. Et même de connaître la distance d’Évreux à Milano, puisque dans ce type de triangle l’hypoténuse est avec le grand côté de l’angle droit dans un rapport de 18 à 17 :

• 725 / 18 = 40,27 ; 684 / 17 = 40,23 (x 18 = 724,2 : l’écart est de moins d’un km).

Samoreau

Venons‑en maintenant à Samoreau, en territoire sénon. Géographiquement, cette portion de la vallée de la Seine correspond à la plus petite distance entre la Loire et la Seine (Desbordes, 1971). Entre les deux fleuves, une route commerciale devait partir de Briare (Brivodurum, le « Marché du pont »), au sud exact de Samoreau, puis remonter jusqu’à Montargis et gagner la Seine par le Loing. La région de Samoreau devait donc se situer sur une importante voie commerciale. Mais pourquoi le Montmélian qui nous intéresse est‑il situé sur le rocher de Samoreau, plutôt qu’à Saint-Mammès au confluent du Loing et de la Seine, ou sur les coteaux de Champagne-sur-Seine, à quelques kilomètres en amont de Samoreau ? La réponse, là encore, pourrait être d’ordre géodésique.

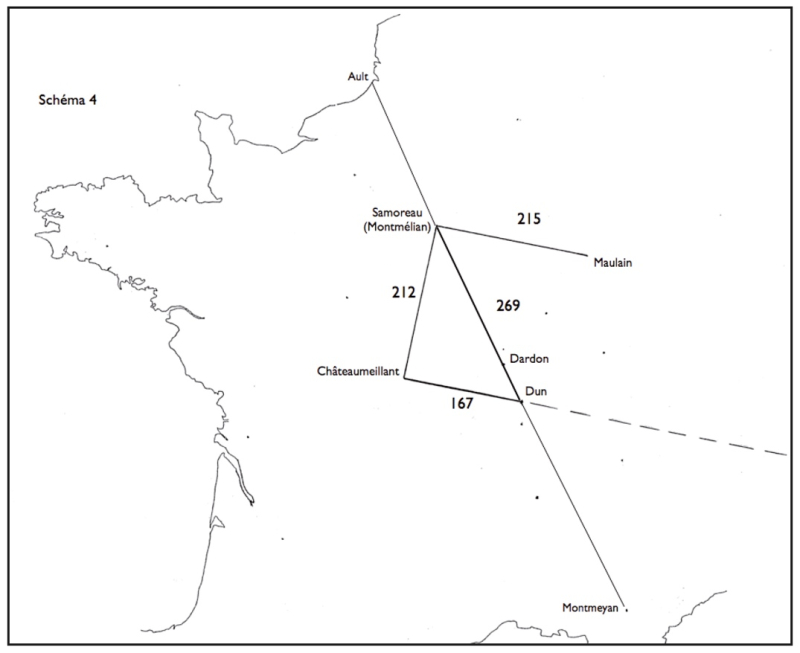
On arrive à Samoreau, comme je l’ai dit, en suivant la direction Dun – Dardon, sur la grande Diagonale. Mais on y arrive aussi à partir de Châteaumeillant, en traçant simplement une perpendiculaire à la direction Milano – Châteaumeillant : Samoreau se situe au point de convergence de ces deux lignes (fig. 4).

Figure 4.

Considérons le triangle rectangle Châteaumeillant – Samoreau – Dun. Ses trois côtés font respectivement 212,6 km, 269,5 km (pour l’hypoténuse Dun – Samoreau) et 167,4 km. Si l’on calcule le rapport entre ces trois distances, on constate qu’il est de l’ordre de 11/14 (= 1,27) : ce sont les proportions du « triangle pyramide ».

Traçons maintenant une nouvelle perpendiculaire (donc une parallèle à la ligne de base Dun – Châteaumeillant). On arrive alors au Mediolanum de Maulain (Haute‑Marne), chez les Lingons.

Maulain est l’exemple même d’un Mediolanum déterminé de façon purement géométrique, sans particularité géographique remarquable (ce n’est pas une hauteur, et si la source de la Meuse est proche, elle n’est pas à Maulain même). Il répond en revanche à plusieurs contraintes géométriques (ou géodésiques), qui le mettent notamment en relation avec Mâlain en Côte‑d’Or (fig. 5).

Figure 5.

On connaît la cité gallo-romaine de Mâlain – Mediolanum, dont un quartier a été fouillé très minutieusement par Louis Roussel (1988) ; mais le point de repère ancien était peut‑être plutôt le Signal de Mâlain, ancien éperon barré qui est un des points culminants du Seuil de Bourgogne, à la limite méridionale du Bassin parisien.

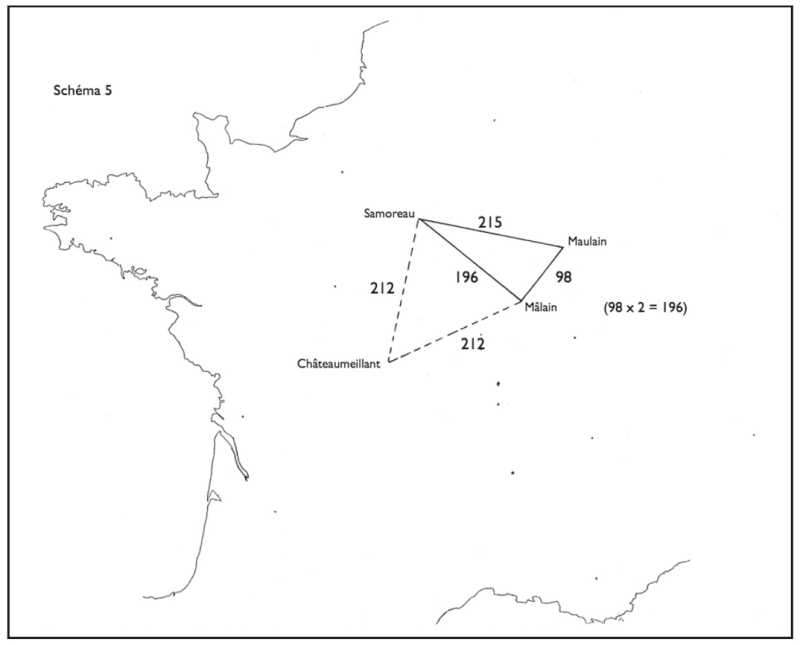
Première constatation : Mâlain, Châteaumeillant et Samoreau forment un triangle isocèle, dont les deux côtés égaux ont une longueur de 212 km.

Deuxième constatation : Mâlain, Samoreau et Maulain forment un triangle rectangle 1 x 2 : le petit côté de l’angle droit, Mâlain – Maulain (98 km), est en effet la moitié du grand, Mâlain – Samoreau (196 km) : 98 x 2 = 196.

Ce n’est pas tout. J’ai dit que les directions de base étaient recroisées par les axes cardinaux. On a vu qu’au sud de Samoreau se trouvait Briare. Briare n’est pas un Mediolanum. Mais si l’on traverse la Loire, on trouve sur la rive gauche, en face de Briare, un micro-toponyme significatif : Les Plantes Milan à Saint-Firmin-sur-Loire.

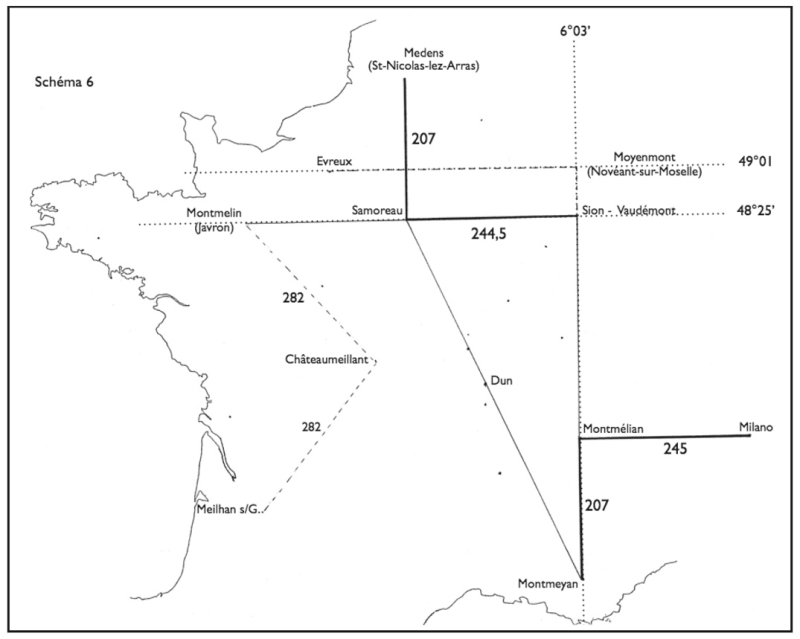
Cependant, le plus intéressant est la branche nord de cette ligne N‑S. Elle relie Samoreau à l’ancien Mediolanum de Medens, devenu Saint-Nicolas dans la banlieue nord d’Arras. La distance qui sépare Samoreau de Saint-Nicolas, calculée à partir de la différence de latitude (1° 52’) est de 207,4 km (1’ de latitude correspondant à une distance de 1,852 km, 1° 52’, soit 112’ = 207,424 km) [fig. 6].

Figure 6.

Cette différence de latitude est exactement celle qui sépare deux autres Mediolanum situés sur un même méridien : Montmeyan dans le Var, à l’extrémité de la grande Diagonale (lat. 43° 38’), et Montmélian en Savoie au bord de l’Isère (45° 30’). Même écart de 112’ en latitude et donc même distance : 207,4 km. On pourrait n’y voir qu’une coïncidence si ce Montmélian n’offrait pas en outre la particularité de se situer sensiblement à la latitude de Milano (45° 30’ contre 45° 28’ pour le centre de Milano). D’où une remarquable équerre dont la branche nord-sud (Montmélian – Montmeyan) vaut 207 km et la branche est-ouest (Milano – Montmélian), 245 km.

On est alors conduit à se demander s’il n’existerait pas une équerre symétrique à partir de Samoreau. J’ai d’abord pensé que cette équerre était assurée du côté ouest par le lieu-dit Montmelin, aujourd’hui une ferme (un élevage de poulets), à l’extrémité de la commune de Javron en Mayenne, sur le parallèle de Samoreau — parallèle qui passe par étampes et par les quartiers sud de Chartres. Le toponyme n’offre aucune garantie. Javron mérite cependant d’être considéré. Sa distance à Châteaumeillant est égale à la distance de Châteaumeillant à Meilhan-sur-Garonne (282 km dans les deux cas) : c’est peut‑être ce qui a déterminé sa position. En revanche la distance Samoreau – Javron (228 km) semble quelconque. Elle ne permet pas de construire un triangle qui expliquerait l’égalité Montmélian – Montmeyan et Samoreau – Saint-Nicolas. Cherchons donc à l’est. On n’y trouve aucun toponyme de type « milieu ». Mais à une distance égale à celle de Montmélian – Milano (soit 245 km), on tombe au milieu du plateau lorrain sur un haut-lieu célèbre, site d’oppidum sacralisé depuis la Préhistoire : la colline de Sion-Vaudémont (la « Colline inspirée » de Barrès), hauteur en forme de L dont une extrémité correspond au Signal de Vaudémont et l’autre au site de Sion, occupé de façon continue depuis le Néolithique.

Se dessinent ainsi deux triangles rectangles égaux, symétriques et subtilement inversés : les deux plus longues branches partent de l’est (Milano, Sion), et les branches perpendiculaires partent l’une vers le sud à quelque distance de la Méditerranée, l’autre vers le nord, à quelque distance de la Manche.

Résumons :

• la latitude de Sion est celle de Samoreau (48° 25’) ;

• sa longitude (6° 5’) est assez exactement celle de Montmélian, Savoie (6° 3’) et exactement celle de Montmeyan, Var (6° 5’) ;

• lignes E‑O : la distance Sion – Samoreau (calculée 244,5 km) vaut la distance Montmélian – Milano (245,4 km) ;

• lignes N‑S : la distance Montmélian – Montmeyan (207 km) est égale à la distance Samoreau – Medens (Saint-Nicolas-lez-Arras, 207 km).

De telles égalités, à la fois de distances, d’orientation et de coordonnées, excluent le jeu du hasard. Elles justifient et même imposent d’ajouter la colline de Sion à la liste volontairement restreinte des hauts-lieux, dont on peut affirmer le rôle d’observatoire et de repère dans l’établissement du réseau géodésique à grande échelle que l’on voit peu à peu se constituer.

Le méridien Montmeyan – Sion peut même être prolongé en direction du nord, jusqu’au parallèle d’Évreux (49° 01’) : le croisement de ces deux lignes correspond à l’agglomération de Novéant-sur-Moselle (Novientum en gaulois, selon Dauzat-Rostaing), où se trouve un Moyenmont qui n’est peut‑être pas là par hasard.

Rosaces

D’autres directions seraient encore à considérer : les directions formant des angles de 60° par rapport aux axes N‑S (et par conséquent de 30° par rapport aux axes E‑O). On aboutit ainsi, à partir des points pivots les plus importants, à des sortes de rosaces. Je me contenterai de les survoler faute de temps.

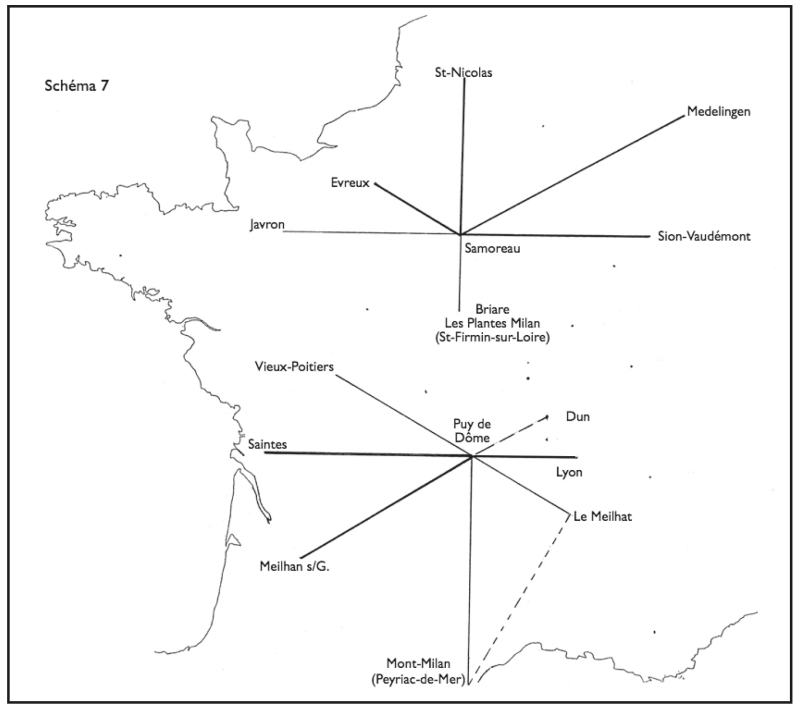
Si l’on joint sur une carte Samoreau à Évreux, on s’aperçoit que la ligne fait un angle de 60° avec l’axe N‑S (fig. 7). Partant de Samoreau en direction du nord-est, une ligne beaucoup plus longue forme un angle symétrique qui fait passer des bords de la Seine aux bords de la Moselle, via le Camp de Châlon, pour rejoindre chez les Trévires, en aval de Trèves, un Mediolanum dont parle le poète Fortunat6, et qui correspond aujourd’hui au site de Medelingen, signalé par Holder au confluent de la Moselle et de la Trohn, près de Neumagen (mais rien ne l’indique sur place, et ce n’est même pas un village).

Figure 7.

Medelingen se situe au croisement de cette direction et d’une autre, partant de Molain et perpendiculaire à la direction de base Milano – Dun.

On retrouve des dispositifs analogues, centrés respectivement sur le Puy-de-Dôme et sur la Montagne de Dun.

Dans le cas du Puy-de-Dôme, l’axe E‑O apparaît fondamental : c’est le parallèle commun au Puy-de-Dôme, à Lyon et à Saintes, correspondant au futur tracé de la route d’Agrippa (futur, dans la mesure où l’on peut penser que le Mediolanum des Santons existait avant la conquête). Vers le sud, le repérage du méridien semble assuré par l’existence d’un Mont-Milan à côté de Peyriac-de-Mer, au sud de Narbonne (au bord de l’étang de Sigean et proche de l’abbaye de Fondfroide). La ligne est balisée par plusieurs lieux-dits en Méjane (« milieu » en langue d’oc) : Le Méjanel à Recoules-Prévinquières (Aveyron), un Ravin de Méjanels juste avant la traversée du Tarn à l’ouest de Millau, un Méjanel et Ruisseau de Méjanel à Fayet (toujours dans l’Aveyron). Je sais bien que les Méjan, Méjane, Méjanel foisonnent dans la région. Ce n’est pas une raison pour se dispenser de noter ceux qui se situent exactement sur le méridien du Puy-de-Dôme.

Pourquoi s’être arrêté à Peyriac-de-Mer alors que l’axe aurait pu descendre encore plus bas en direction de Perpignan ? Une réponse possible peut être fournie par la position de ce Mont-Milan par rapport au Meilhat dans l’Ardèche (milieu, je le rappelle, de la ligne Milano – Meilhan-sur-Garonne). Là encore, un Sommet de Méjan à La Souche (Ardèche) situé sur la ligne fait figure de relais ou de point de visée. Mais l’important est que l’angle formé avec la ligne Puy-de-Dôme – Le Meilhat est un angle droit. Cette ligne étant elle-même à 60° du méridien, on obtient un magnifique triangle dit « platonicien » : la moitié d’un équilatéral, dont le petit côté vaut la moitié de l’hypoténuse. Ici à 3 km près (300 / 147).

Vers le nord, aucun toponyme significatif sur le méridien du Puy-de-Dôme7. On peut donc considérer que les deux dispositifs centrés l’un sur le Puy-de-Dôme, l’autre sur Samoreau sont largement symétriques et inverses, tournés l’un vers le sud, l’autre vers le nord du territoire.

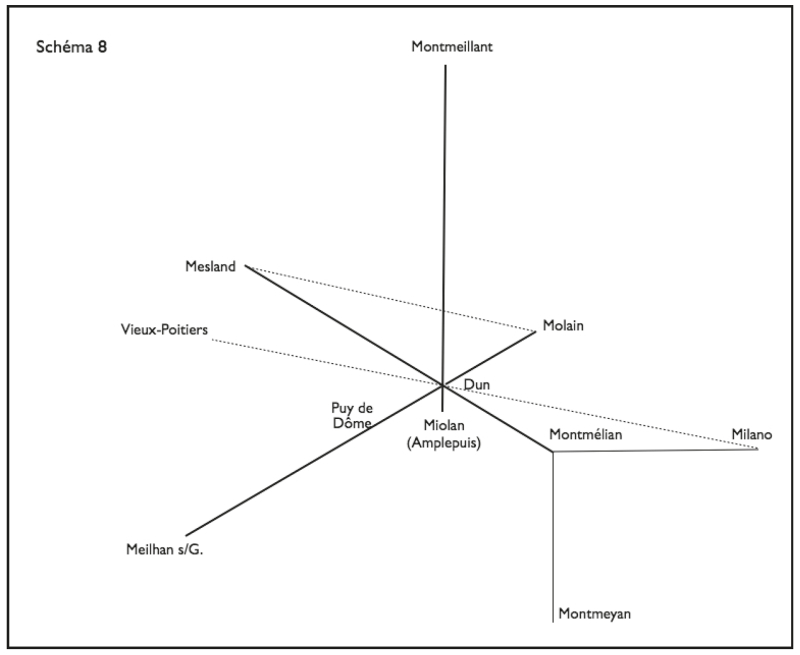
La « rosace » de Dun, quant à elle, s’impose au contraire à partir de l’axe N‑S (fig. 8).

Figure 8.

C’est cet axe qui me conduisit à découvrir l’importance de la Montagne de Dun, lorsque je constatai sur des relevés que m’avait fournis l’IGN que le site de Miolan à Amplepuis, au sud de Dun, et Montmélian dans les Ardennes avaient exactement la même longitude (4° 20’E). Cette espèce de méridienne éduenne, prolongée à travers le territoire des Lingons jusque chez les Rèmes, est remarquablement balisée par la Montagne de Bar, puis par Montbard, par l’oppidum de Vertillos sur la commune de Vertault (au point de rupture de charge entre les bassins de la Seine et de la Saône) ; on arrive ensuite à Châlons-en-Champagne, à Rethel, enfin à Montmeillant à 382 km de la Montagne de Dun.

Formant des angles de 60° sur cet axe N‑S, deux grandes lignes : la ligne Meilhan-sur-Garonne – Puy-de-Dôme – Dun – Molain (moyennant la légère distorsion que j’ai signalée) ; et la ligne Montmélian (Savoie) – Mesland (Loir-et-Cher)8.

On ne repère en revanche aucun axe E‑O centré sur Dun. Il est remplacé, si l’on peut dire, par notre ligne de base Milano – Châteaumeillant, décalée d’environ 11° par rapport à l’axe des équinoxes.

Extensions

Sans chercher à reconstituer artificiellement une chronologie pour laquelle les données, actuellement, font presque entièrement défaut, on peut supposer raisonnablement une extension progressive des repérages à partir des centres éduens, sénons, arvernes et bituriges, avec la volonté d’unifier le système et de l’étendre à l’ensemble du territoire — avec peut‑être aussi l’espoir de l’englober dans une vaste structure géométrico-symbolique.

Les perpendiculaires que nous avons commencé à repérer sur la ligne de base Milano – Dun sont le début d’une sorte de quadrillage qui se laisse compléter par d’autres lignes.

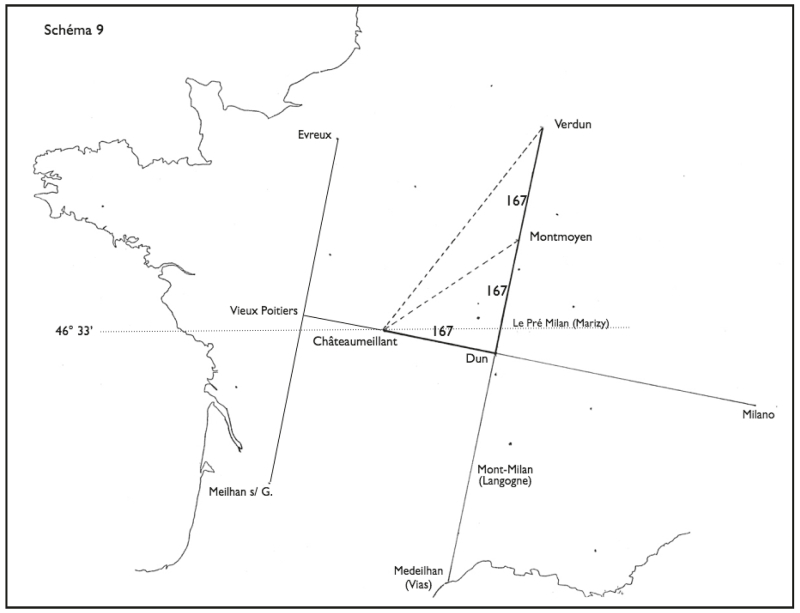
Verdun (fig. 9)

C’est ainsi qu’une perpendiculaire partant de Dun conduit à la commune de Montmoyen (Côte‑d’Or), de manière à former avec Châteaumeillant un triangle rectangle isocèle (166,6 km vers Montmoyen, 167,4 km vers Châteaumeillant). On note que le croisement de cette ligne avec le parallèle de Châteaumeillant (46° 33’) est marqué par un lieu‑dit, le Pré Milan à Marizy. Prolongée de 167 km vers le nord, la ligne arrive à Verdun (la « Grande Forteresse » ou la « Forteresse par excellence »). Si l’on tient compte de Verdun, on passe donc d’un triangle rectangle isocèle à un triangle rectangle 1 x 2 (fig. 9). Prolongée vers le sud, cette même perpendiculaire arrive au Mont-Milan de Langogne (qui mériterait un développement à lui tout seul), passe par le massif du Lozère, le massif de l’Aigoual, et parvient finalement à la côte méditerranéenne dans la commune de Vias (Hérault), où se trouve un Médeillan que les étymologistes répugnent à rattacher à Mediolanum, mais qui s’intègre singulièrement bien au système.

Figure 9.

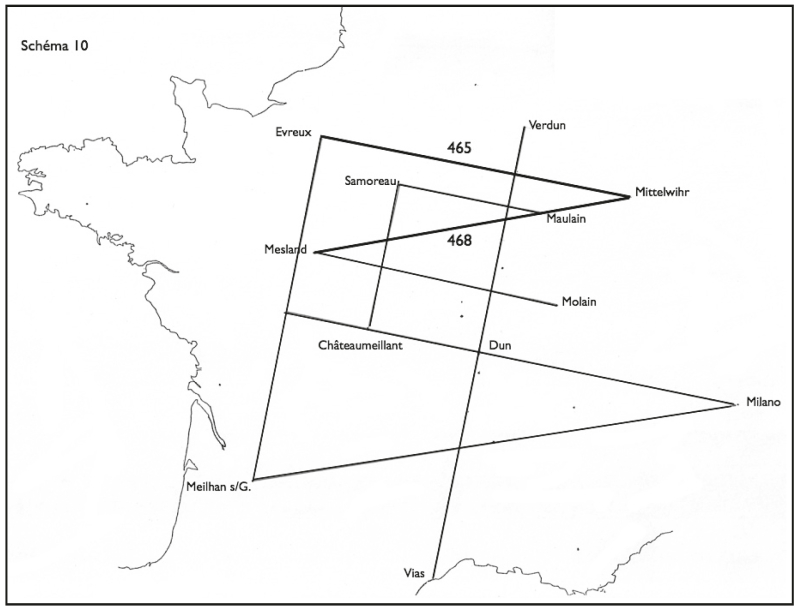
Construction de Mittelwihr (fig. 10)

À partir d’Évreux, une parallèle à la ligne de base conduit jusque dans l’Alsace actuelle (chez les Rauraques ?). On trouve là le village de Mittelwihr (« la ferme du milieu »), au nord de Colmar. On y a trouvé les vestiges d’une villa romaine et une pierre d’autel datée de 204 apr. J.‑C. Mittelwihr se trouve exactement au point de jonction de cette ligne d’Évreux (parallèle à Samoreau – Maulain), et d’une ligne partant de Mesland (Loir-et-Cher), passant par Maulain et faisant avec la précédente un angle d’environ 20°, donc elle‑même parallèle à Milano – Meilhan-sur-Garonne. J’ajoute qu’Évreux et Mesland se trouvent sensiblement sur la même longitude et que les distances de ces deux points à Mittelwihr sont comparables (Évreux – Mittelwihr = 465 km ; Mesland – Mittelwihr = 468 km).

Figure 10.

On retrouvera plus loin ce Mittelwihr. Mais il peut déjà nous en apprendre beaucoup sur la manière dont les Mediolanum (ou du moins certains d’entre eux) étaient déterminés : tout indique qu’ils étaient situés aux points de rencontre de deux directions préalablement définies. Plus que des milieux sur une droite, ce seraient des points de convergence, de conjointure de deux ou plusieurs droites, en même temps (pour les plus importants d’entre eux) que des points de départ vers de nouvelles directions.

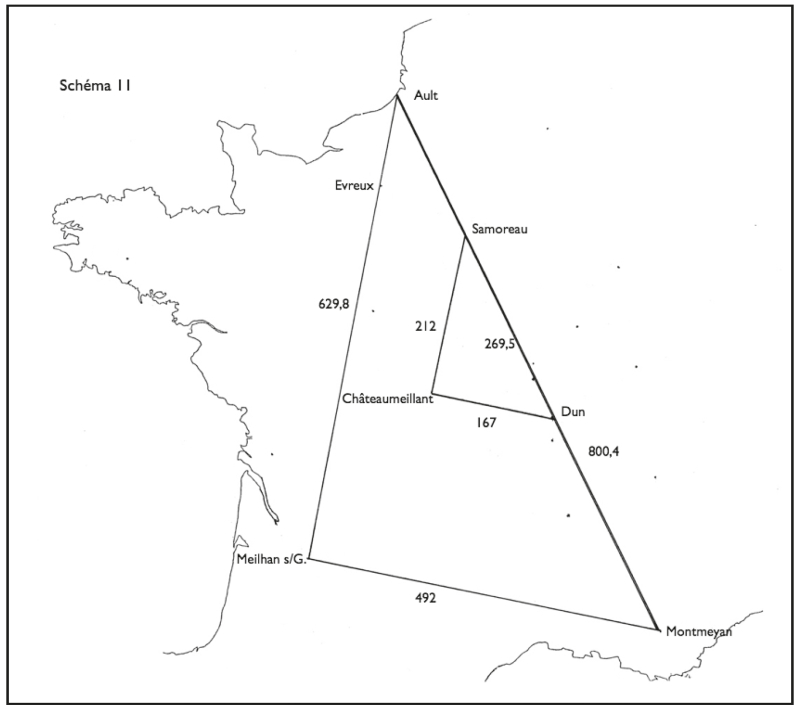
Ault (fig. 11)

À l’ouest, reprenons la grande perpendiculaire Meilhan-sur-Garonne – Évreux et prolongeons‑la jusqu’à la côte (fig. 11). Comme par hasard, on arrive à Ault qui est aussi le point d’aboutissement de la grande Diagonale. Et si l’on joint Meilhan-sur-Garonne à Montmeyan (l’autre extrémité de la Diagonale), on obtient un immense triangle rectangle, l’angle à Meilhan étant un angle droit. Et un triangle rectangle remarquable : c’est en effet un triangle « égyptien » ou « pyramide », semblable par conséquent à celui que nous avons déjà repéré entre Dun, Châteaumeillant et Samoreau. Semblable et de côtés parallèles, la disposition de ces deux triangles imbriqués l’un dans l’autre répond à ce que les anciens géomètres, de tradition pythagoricienne, nommaient un gnomon.

Figure 11.

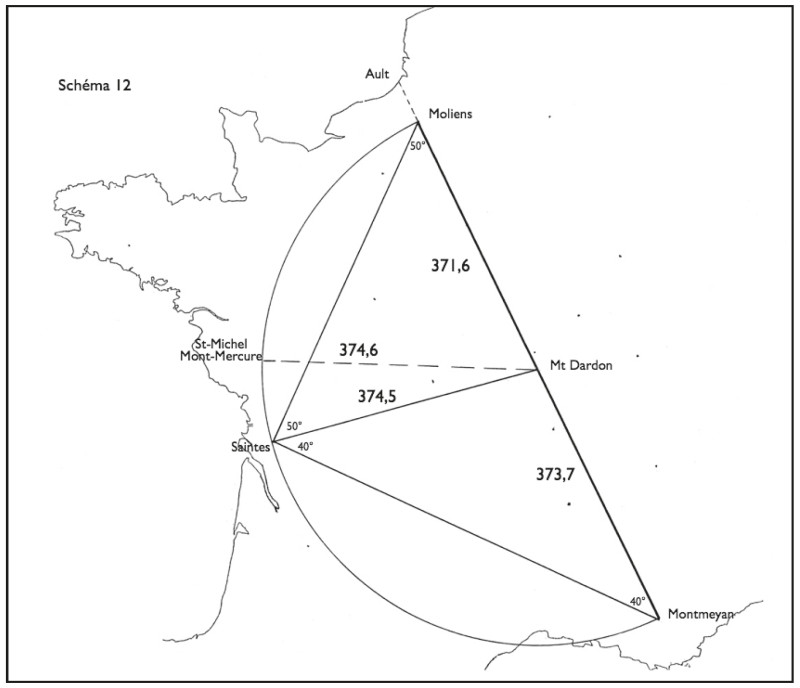
Mont Dardon (fig. 12)

Par ailleurs, si l’on joint Saintes à Moliens et à Montmeyan, on obtient un autre immense triangle rectangle avec angle droit à Saintes ; le Mont Dardon marque le milieu de l’hypoténuse (fig. 12). La ligne Saintes – Dardon partage cet angle droit en deux angles respectivement de 40° et de 50°. D’où deux triangles isocèles :

• Dardon – Montmeyan (373,7 km) = Dardon – Saintes (374,5 km) (= Dardon – Saint-Michel-Mont-Mercure, point culminant de la Vendée : 374,6 km) ;

• Dardon – Saintes = (plus approximativement) Dardon – Moliens (371,6 km).

Figure 12.

Situation de Meslan

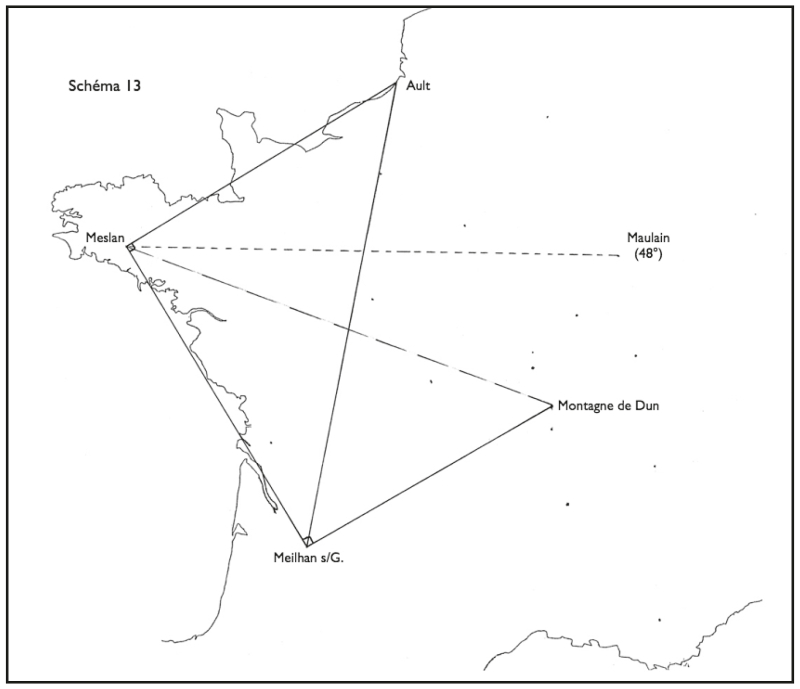
Reste à intégrer au système la partie la plus occidentale du territoire, avec la Bretagne. En ce qui concerne celle‑ci, un unique point y pourvoit (le seul dont le toponyme dériverait avec certitude de Mediolanum) : la commune de Meslan, à la frontière du Finistère et du Morbihan. On peut dire que la position de ce Meslan est un véritable chef-d’œuvre (fig. 13).

• Il se trouve à la latitude de Maulain, à une minute près : 47° 59’ / 48° (les Anciens étaient parfaitement capables de déterminer une latitude sans avoir à traverser tout le territoire). Ce rapport à Maulain le rattache indirectement à la ligne Puy-de-Dôme – Dardon – Sion et au système de Samoreau.

• Une ligne Meslan – Meilhan-sur-Garonne forme un angle droit avec la ligne Montagne de Dun – Meilhan-sur-Garonne, elle‑même symétrique, on l’a vu, de Dun – Milano. Cette ligne traverse la Gironde, passe par le site du Fâ, puis elle suit au plus près la côte à partir de l’embouchure de la Seudre, traverse l’île d’Oléron dans sa plus grande longueur, et retrouve la terre ferme à Locmariaquer.

• À Meslan, cette même ligne de la côte fait un nouvel angle droit avec une ligne donnant la direction de la Manche jusqu’à Ault (et par conséquent parallèle à Dun – Meilhan-sur-Garonne). L’hypoténuse de ce nouveau grand triangle rectangle nous est connue, puisque c’est l’envers (si l’on peut dire) de la ligne Meilhan-sur-Garonne – Évreux – Ault qui permettait de construire le grand triangle égyptien.

Figure 13.

Meillant

Peut‑on maintenant imaginer un site qui serait à la fois équidistant de Saintes, d’Évreux et de Maulain, de Samoreau et de Mâlain, de Mittelwihr et de Saint-Nicolas-lez-Arras, de Molain et du Mont-Milan de Langogne, de Meslan de Bretagne et de Medelingen ? Ce site existe, et il se nomme Meillant.

Il se trouve à 34,7 km au nord-est de Châteaumeillant. On y voit un beau château Renaissance construit, au retour des guerres d’Italie, par Charles II d’Amboise, seigneur de Chaumont, qui fut gouverneur de Milan sous Louis XII (ce qui faisait dire à l’époque « Milan a fait Meillant »…). On y a découvert des vestiges d’époque romaine, une statue très mutilée du dieu gaulois aux sabots de cerf, mais rien de comparable à l’oppidum de Châteaumeillant. Ce qui conduit à penser que Meillant est plus tardif. Il est tentant d’y voir le point d’achèvement de l’entreprise de balisage du territoire gaulois, à une époque où celui‑ci était unifié et correspondait pour l’essentiel au territoire de la France actuelle (avec en plus une pointe dans la vallée de la Moselle jusqu’à la région de Trèves). Coïncidence frappante : Meillant se trouve à environ 5 km de la localité de Bruère-Allichamps, considérée comme le « centre de la France » ; ce centre fut matérialisé par un milliaire romain installé au milieu de la place du village, et plus récemment par une construction en bordure de l’autoroute qui présente une petite exposition permanente sur ce thème.

Meillant est équidistant (fig. 14) :

• du Mont Dardon et du Puy-de-Dôme (117 – 117,6 km) ;

• de la Montagne de Dun et du Vieux-Poitiers (151,7 – 152,6 km), ce qui le rattache à la ligne de base Milano – Dun – Châteaumeillant – Vieux-Poitiers ;

• de Samoreau (184 km), Mâlain (183,7 km), Miolan à Hurigny (banlieue nord de Mâcon, sur le méridien de Lyon, 182,4 km), du Miolan à Pontcharra-sur-Turdine, anciennement village de Saint‑Loup (Rhône, ce serait le Mediolanum indiqué dans cette région par la Table de Peutinger – 183 km) ;

• de Molain (252 km) et du Mont-Milan de Langogne (253,4 km) ;

• de Saintes (268 km), d’Évreux (269 km) et de Maulain (270,3 km). Meillant se trouve donc sur la bissectrice de l’angle de 60° Saintes – Dun – Évreux, relativement facile à construire.

En outre la ligne Meillant – Maulain croise le méridien de Lyon – Hurigny à Montmoyen, qui marque par ailleurs, comme on l’a vu, la mi‑distance exacte de Dun à Verdun.

La ligne Saintes – Meillant prolongée conduit à Mittelwihr, en passant par la Croix-Milan dans le Morvan, au croisement du méridien du Mont-Milan de Langogne.

• Mittelwihr lui‑même se trouve à la même distance de Meillant que Saint-Nicolas-lez-Arras sur le méridien de Samoreau, et que Médeillan à Vias. La ligne Vias – Meillant – Ault est une droite.

• Dernier cercle d’équidistances, le plus vaste et le plus étonnant : il englobe Meslan (466,7 km) et Medelingen (472 km), en passant par la pointe du Cotentin et la région de Calais.

Figure 14.

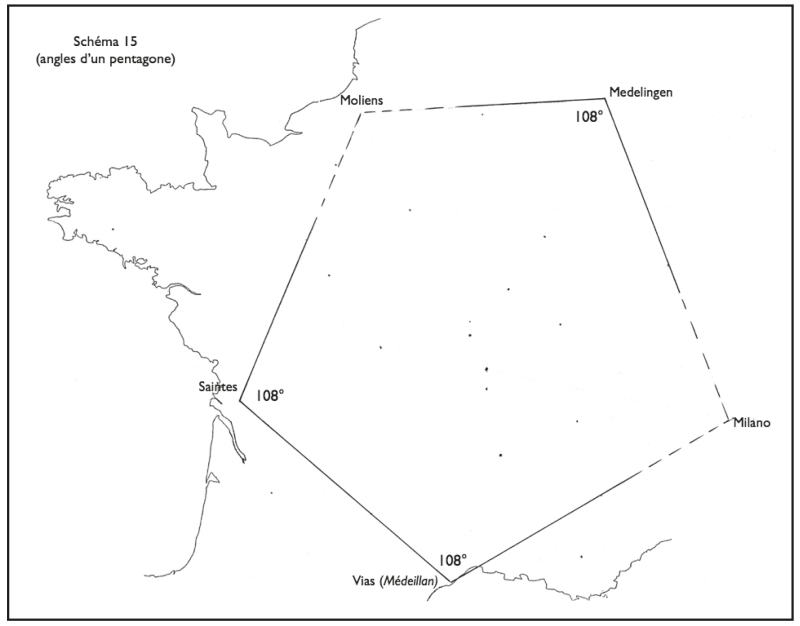
La situation de Meillant doit obéir à une clé géométrique que je n’ai pas su retrouver, mais qui semble nécessaire pour expliquer une aussi surprenante construction. Les druides auraient‑ils cherché à englober l’ensemble du territoire dans une figure géométrique unique ? On peut s’interroger. L’existence d’angles de 108° (angle du pentagone) en des points-clés du système conduit à se demander s’ils n’ont pas essayé d’enfermer le territoire gaulois dans un vaste pentagone régulier (figure difficile à construire mais particulièrement sacralisée, comme on sait, dans la tradition pythagoricienne). Ils ne semblent pas y être parvenus, trois seulement des angles du pentagone que l’on peut tracer à partir de Milano, Vias, Meilhan-sur-Garonne, Moliens et Medelingen étant égaux à 108° (fig. 15).

Figure 15.

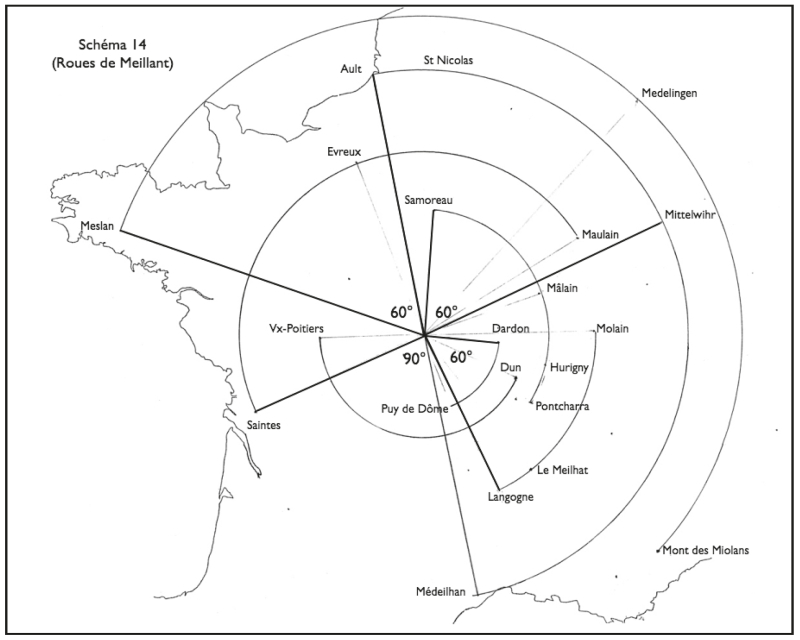
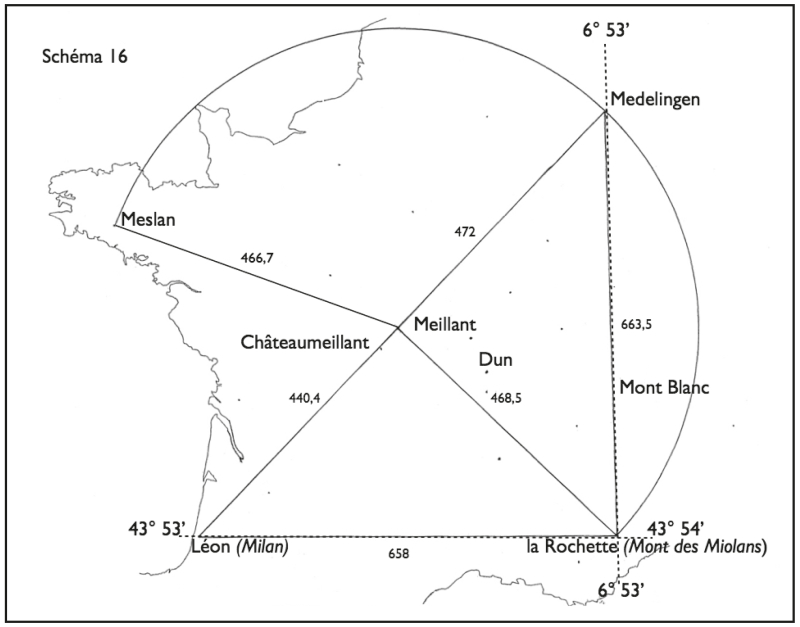
Peut‑être s’en sont‑ils tenus à la figure simple d’un carré incomplet orienté selon les points cardinaux (fig. 16). Partons de Medelingen, qui en marquerait le coin nord-est. Le méridien de Medelingen (6° 53’) passe par Moyenmoutier (Vosges), devenu au Moyen Âge une très importante abbaye. Puis par le massif du Mont-Blanc (6° 52’). Ce même méridien rencontre dans les Alpes maritimes, à La Rochette, une Montagne des Miolans qui culmine à 995 m au sud de Puget-Théniers. On constate que la Montagne des Miolans est sensiblement à la même distance de Meillant (468,5 km) que Meillant de Medelingen (472 km). Cette nouvelle ligne passe par le Mont Miolan de Souternon (Loire) et par un Champ du Milan à Saint-Pourçain-sur-Sioule, à 80 km de Meillant. L’angle Medelingen – Meillant – Montagne des Miolans fait 90°. D’où un immense triangle rectangle isocèle, moitié d’un carré.

Figure 16.

Impossible de compléter le carré, puisque le quatrième sommet tomberait dans la mer. Mais côté sud-ouest, si l’on prolonge la direction Medelingen – Meillant jusqu’à la côte Atlantique, on arrive à une latitude proche de celle de la Montagne des Miolans (à 1’ près : 43° 54’ – 43° 53’), à proximité du village de Léon. Et à Léon se trouve, à 3 km au sud du bourg, le hameau de Milan, qui est un des deux « Milan » des Landes. Le second hameau de Milan appartient à la commune de Saint-Pierre-du-Mont, faubourg de Mont-de-Marsan, et il se trouve à la même latitude.

Conclusion

On voit quelles énormes questions posent ces différentes constatations — car ce ne sont que des constatations, dûment vérifiées.

Expliquer l’ensemble de ces constructions par des rencontres aléatoires et de simples coïncidences est difficilement soutenable. On peut seulement admettre que certaines coïncidences géographiques (par exemple l’identité de latitude de Samoreau et de la colline de Sion) ont été repérées et systématiquement exploitées par les druides spécialisés dans ce travail sur le terrain.

Par ailleurs, la chronologie de cette espèce de géodésie resterait à préciser. Combien de siècles son élaboration a-t-elle pu demander ? Lorsqu’on passe de Châteaumeillant à Meillant, on a le sentiment de changer de monde. Le système ne s’organise plus en fonction d’un peuple (le peuple éduen) soucieux de manifester sa primauté, mais en fonction d’un territoire unifié dont il s’agirait de trouver le centre exact.

Les principes de construction de cette géodésie sont bien différents de ceux que suivaient les Romains dans leurs entreprises de centuriations. Mais rien ne dit qu’une partie des lignes repérées ne date pas de l’époque romaine — de même que le calendrier de Coligny perpétue en pleine époque romaine des principes calendaires qui remontent bien plus haut. Cela suppose des traditions et des pratiques transmises sur plusieurs générations par des confréries d’origine druidique, et de type compagnonnique (on songe aux sodalicia dont parlait Timagène selon Ammien Marcellin, XV, ix, 8). Quelques éléments de ces traditions ont pu perdurer assez tard, jusqu’en plein Moyen Âge. Dans la littérature celtique, on en trouve un dernier écho dans le conte de Llud et Lleuelys du Mabinogi, lorsque le « roi de France » conseille à son frère Llud, roi de Grande-Bretagne, de faire mesurer l’île en longueur et en largeur, et d’en trouver le centre exact pour se débarrasser des dragons qui se battent dans le ciel chaque nuit de 1^er mai. Ce n’est peut‑être pas un hasard si c’est le souverain régnant sur l’ancienne Gaule qui donne ce conseil au roi de Grande-Bretagne. Car même s’il existe des Mediolanum hors de Gaule qui demanderaient à être examinés dans la même perspective, tout indique que c’est bien en Gaule que les druides ont mené le plus loin, et avec le plus de constance, leurs recherches de terrarum magnitudine.